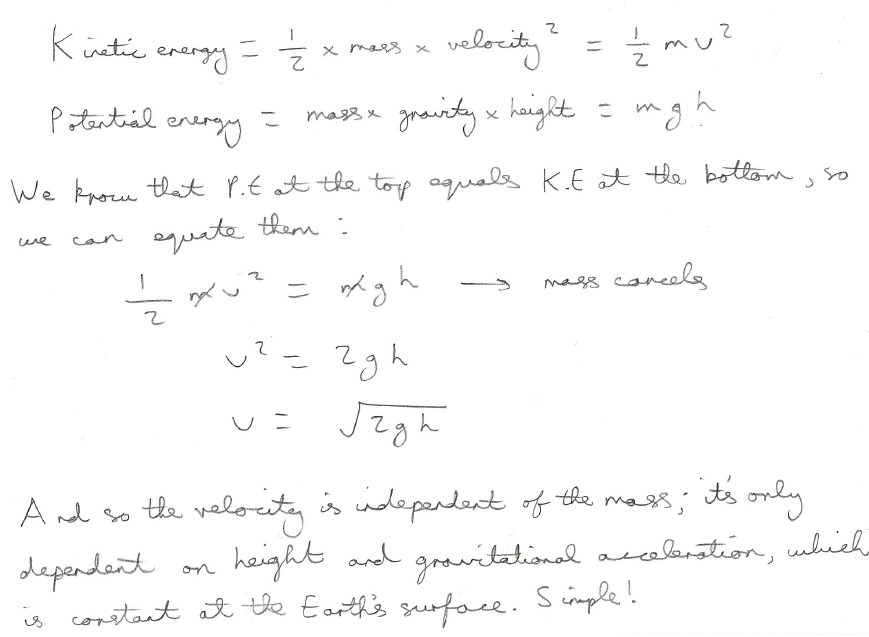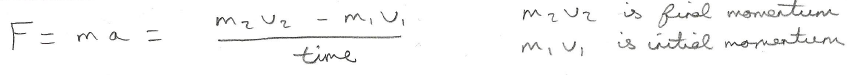|
|
|
The Physics of Theme Parks
The Hammer and the Feather – Why things fall at the same rate
First off, as a disclaimer, I have to admit I’m going to contradict myself a little in this article. But fret not, it should (I really hope) all make sense in the end, it’s just that there are a lot of things we have to take into account.
So what the hell have hammers and feathers got to do with anything? Well, as you may know, there was a famous physics experiment that took place on the moon during the Apollo 15 mission. Astronaut James Scott dropped a geological hammer and a feather from the same height and they hit the moon’s surface at the same time. It demonstrates the concept that in a vacuum all objects are acted on by gravity the same amount, and so all things fall at the same rate. The experiment was conducted in its extraterrestrial setting in order to negate the effects of aerodynamic drag, a friction between the objects and the air; of course if it was done on earth the feather would’ve have taken far longer to fall because of its large surface area compared to its mass (remember ‘mass’ is what we measure in kg or pounds, and is what we commonly think of as ‘weight’. In actuality weight is slightly different; it’s a force, measured in Newtons, and Weight = Mass*Gravity).
We can prove why this is with some straightforward high school physics to do with energy. There are two main forms of energy when it comes to a moving object (formally called a projectile, our roller coaster car): Kinetic energy (KE) and gravitational potential energy (GPE). KE is the energy derived from the projectile’s velocity and GPE is derived from its height:
First off, as a disclaimer, I have to admit I’m going to contradict myself a little in this article. But fret not, it should (I really hope) all make sense in the end, it’s just that there are a lot of things we have to take into account.
So what the hell have hammers and feathers got to do with anything? Well, as you may know, there was a famous physics experiment that took place on the moon during the Apollo 15 mission. Astronaut James Scott dropped a geological hammer and a feather from the same height and they hit the moon’s surface at the same time. It demonstrates the concept that in a vacuum all objects are acted on by gravity the same amount, and so all things fall at the same rate. The experiment was conducted in its extraterrestrial setting in order to negate the effects of aerodynamic drag, a friction between the objects and the air; of course if it was done on earth the feather would’ve have taken far longer to fall because of its large surface area compared to its mass (remember ‘mass’ is what we measure in kg or pounds, and is what we commonly think of as ‘weight’. In actuality weight is slightly different; it’s a force, measured in Newtons, and Weight = Mass*Gravity).
We can prove why this is with some straightforward high school physics to do with energy. There are two main forms of energy when it comes to a moving object (formally called a projectile, our roller coaster car): Kinetic energy (KE) and gravitational potential energy (GPE). KE is the energy derived from the projectile’s velocity and GPE is derived from its height:
But this isn’t the whole story. Sure, the physics is correct, but obviously there are some factors other than just one dimensional energy analysis. If anyone has been to a theme park when a new ride is being built, you may have seen it running with crash dummies. These dummies are filled with water to give an accurate representation of how the ride will behave with a fully loaded train. If mass made no difference at all then this would be a pointless exercise. With roller coasters the point about air resistance isn’t very relevant; there will be little difference in aerodynamics between a loaded or an unloaded train, but there are other, less obvious ideas going on, and I’ll mention two key ones here.
One is friction between the wheels and the track. This is a big issue as the wheels on a roller coaster are clamped onto the track in order to keep the ride safe and without too much of a rattle. Newton’s Third Law famously states that every action has an equal and opposite reaction: the coaster train exerts a force on the track due to its weight (remember weight is the force) and so the track exerts a force back on the train, which we call the normal reaction. The friction force arises because of this normal reaction:
One is friction between the wheels and the track. This is a big issue as the wheels on a roller coaster are clamped onto the track in order to keep the ride safe and without too much of a rattle. Newton’s Third Law famously states that every action has an equal and opposite reaction: the coaster train exerts a force on the track due to its weight (remember weight is the force) and so the track exerts a force back on the train, which we call the normal reaction. The friction force arises because of this normal reaction:
Therefore, as the normal reaction is due to weight, which is due to mass, and friction is due to normal reaction, in this case the motion of the train is affected by its mass.
Brake runs are usually a series of padded blocks which fins on the underside of the train push through, the friction between them slowing the train down. Often cars struggle to make it through brake runs when they’re unloaded; this is because of a lack of momentum:
Brake runs are usually a series of padded blocks which fins on the underside of the train push through, the friction between them slowing the train down. Often cars struggle to make it through brake runs when they’re unloaded; this is because of a lack of momentum:
In order to push through the train needs a certain amount of force. Many of us know from Newton’s Second Law that Force = Mass*Acceleration, but this is misleading because it doesn't take into account the fact that mass can change; it’s better to write force as the rate of change of momentum:
Therefore a greater initial momentum, for which we need a greater mass, will exert a greater magnitude force on the brakes, allowing it to complete its circuit more readily.
So there we have it. The mass of a train generally speaking doesn’t affect how fast it goes, despite what intuition tells us, but there are a few physics principles that mean it’s still a very important factor when designing rides.
So there we have it. The mass of a train generally speaking doesn’t affect how fast it goes, despite what intuition tells us, but there are a few physics principles that mean it’s still a very important factor when designing rides.